Surgimento da Física Moderna
Lei de Faraday para a eletrólise (1833)
É sabido que a dissolução de sal de cozinha na água aumenta consideravelmente a condutividade elétrica da mesma. A interpretação deste fenômeno é que as moléculas NaCl do sal em solução sofrem uma dissociação em sódio Na e cloro Cl, porém com os átomos destes elementos carregados eletricamente, ou seja na forma de íons. Já que a solução é globalmente neutra, os íons de Na e Cl devem possuir cargas iguais e opostas.
Uma eletrólise é realizada com a imersão na solução de dois eletrodos, um positivo (o anodo) e outro negativo (o catodo). Observa-se a passagem de uma corrente pela solução e a acumulação de cloro próximo ao anodo e de sódio próximo ao catodo. Já que cargas opostas se atraem, conclui-se que os íons de cloro estão carregados negativamente e os íons de sódio estão carregados positivamente.
Ao estudar-se a relação entre a quantidade de eletricidade que atravessa o dispositivo de eletrólise e as quantidades de matéria recolhidas nos eletrodos, observa-se que para se obter um mol de sódio (23 g) no catodo, a quantidade de eletricidade necessária é sempre a mesma e vale
| 96.500 C = 1 F, | (1-1) |
denominada faraday (F) em homenagem ao descobridor1 desta lei. Como é de se esperar, recolhe-se então um mol de cloro (35,5 g) no anodo. Isto indica que os íons Na+ e Cl- sempre possuem as mesmas cargas, que denotamos por +e e -e, respectivamente.
Como um mol de qualquer substância sempre contem o mesmo número de átomos, qual seja o número de Avogadro NA, tem-se a relação
| F = NA e. | (1-2) |
Se substituirmos o sal de cozinha por clorúrio de cobre CuCl2, verificamos que precisamos de uma quantidade de eletricidade igual a 2 F para acumular um mol de cobre (63,5 g) no catodo e obtemos então dois mols de cloro no anodo. Devemos portanto atribuir a carga +2e ao íon de cobre, que denotamos Cu++. Íons como Na+ e Cl- são chamados monovalentes, ao passo que Cu++ é bivalente. Íons trivalentes, etc, também são encontrados, mas nunca íons cuja carga não seja um múltiplo inteiro de e, que pode ser considerado então como o quantum elementar de carga.
O valor de e pode ser deduzido da relação (1-2) desde que o valor de NA seja conhecido. Com o valor atual
| NA = 6,02 1023 partículas/mol, | (1-3) |
obtem-se
| e = 1,602 10-19 C. | (1-4) |
Em 1874, Stoney2 sugeriu o nome elétron para a quantidade elementar de carga e. Após a descoberta dos raios catódicos [veja adiante], o mesmo nome foi atribuido às particulas que constituem estes raios, e cuja carga é de fato igual a -e.
[1] Michael Faraday, físico e químico inglês, 1791-1867.
[2] George Johnstone Stoney, físico irlandês, 1826-1911.
Raios catódicos - Medidas de e/m
As descargas elétricas num gás foram objetos de vários estudos no decorrer do século XIX. No caso de gás contido num tubo de vidro, ao diminuir-se a pressão foi observada a aparição de fluorescência nas paredes da tubo próximas a um catodo metálico aquecido. Verificou-se que um objeto colocado entre o catodo e a parede projeta uma “sombra” nesta fuorescência, o que sugeria que o efeito devia-se à propagação até a parede de raios oriundos do catodo. Estavam descobertos os raios catódicos.
Algumas propriedades destes raios foram logo observadas:
- São capazes de atravessar, sem produzir estragos, películas de vidro ou metal de alguns mícrons de espessura.
- São capazes de aquecer consideravelmente um material.
- Podem ser desviados por um campo eletromagnético.
Ao recolher raios catódicos num eletrômetro, Perrin em 1895 determinou que possuiam carga elétrica negativa. Assim, a possibilidade de os raios serem um fenômeno ondulatório análogo à luz foi descartada e eles passaram a ser considerados como formados de partículas. O principal desafio era então de determinar a massa m e a carga e destas partículas.
Utilizamos a notação e para a carga destas partículas, antecipando o fato de que ela iria revelar-se igual à carga do elétron. Porém, na época, isto não era estabelecido; aliás, nem se sabia se esta carga era a mesma para todos os raios catódicos. Semelhantemente, usamos a notação m para a massa das partículas em questão, massa esta que revelará-se também possuir o mesmo valor para todos os raios catódicos.
Para pequenas partículas percorrendo uma distância curta em altissima velocidade, como é o caso dos raios catódicos num tubo, o desvio produzido pela força peso é absolutamente desprezível. Sendo as partículas carregadas, pode-se obter informação sobre elas pela aplicação de campos eletromagéticos. Porém, é fácil ver que, tal procedimento permitirá determinar apenas a razão entre carga e massa, nunca os valores separados destas grandezas. De fato a segunda lei de Newton com a força de Lorentz formece
 |
para a aceleração de uma partícula, de maneira que o movimento da partículas no campo dependerá apenas das condições iniciais e da razão e/m.
Para medir esta razão, J. J. Thomson3 realizou em 1897 dois experimentos distintos.
- No primeiro experimento, os raios catódicos atravessavam um campo magnético uniforme B, de valor conhecido, perpendicular à sua direção de movimento. Como é sabido, nestas condições, a trajetória das partículas é circular e o seu raio R pode ser obtido igualando a força centrípeta à força magnética:
onde v é a velocidade da partícula.
(1-5)
Além do raio da trajetória, Thomson mediu com um eletrômetro a carga total Q das partículas, e com um calorímetro a sua energia cinética total K. Se N for o número de partículas, devemos ter evidentemente:
(1-6)
Eliminando-se v e N das três equações acima, obtem-se facilmente
(1-7) 
(1-8) - O segundo experimento consistia em duas operações.
- Primeiramente, aplicava-se aos raios catódicos campos elétrico E e magnético B "cruzados", quer dizer, perpendiculares entre si e perpendiculares à direção do feixe. Os valores dos campos eram ajustados de tal maneira que os raios não sofressem nenhum desvio, ou seja, de maneira tal que a força elétrica fosse equilibrada pela força magnética. A condição para tanto é
Assim, a medição dos campos E e B que realizam esta condição permite a determinação da velocidade do feixe,
(1-9) 
(1-10)
- A seguir, o campo magnético era desligado. Como atuava apenas o campo elétrico E na direção transversal Oy (na região entre as placas, de comprimento L), a velocidade vx na direção longitudinal era igual a v, dada por (1-10):
As particulas atravessavam a região entre as placas no tempo
(1-11)
Durante este intervalo de tempo, elas eram sujeitas à aceleração
(1-12)
Portanto, elas sofriam o desvio transversal
(1-13)
Ao sair da região onde atua o campo elétrico, as particulas possuiam a velocidade transversal
(1-14) 
(1-15)
Elas demoravam o tempo
até chegar à tela, em movimento retilíneo uniforme. Portanto, durante esta segunda parte do percurso, elas sofriam o deslocamento transversal adicional
(1-16)
Somando (1-14) e (1-17), obtem-se o deslocamento transversal total do feixe:
(1-17)
Vê-se que, uma vez medidos os campos E e B, e sabendo-se as dimensões L e D características do tubo, é possível deduzir a razão e/m pela determinação do desvio Dy do feixe sobre a tela.
(1-18)
- Primeiramente, aplicava-se aos raios catódicos campos elétrico E e magnético B "cruzados", quer dizer, perpendiculares entre si e perpendiculares à direção do feixe. Os valores dos campos eram ajustados de tal maneira que os raios não sofressem nenhum desvio, ou seja, de maneira tal que a força elétrica fosse equilibrada pela força magnética. A condição para tanto é
- O experimento de Thomson e outros semelhantes, realizados com vários tipos de tubo, com catodos feitos de diferentes metais, fornecem sempre o mesmo valor, dentro das incertezas experimentais. O valor atualmente aceito é
Caso se verificasse - como de fato se verificou - que a carga das partículas é realmente igual à carga elementar (1-4) extraída da eletrólise, teriamos para a massa das partículas:
(1-19)
A título de comparação, a massa do mais leve dos átomos (o átomo de hidrogênio) é
(1-19b)
Vê-se que, uma vez Assim, as partículas dos raios catódicos seriam cerca de 1835 vezes mais leves ainda! Porém, até este ponto, não podemos descartar a possibilidade que as partículas tenham massa comparável em grandeza com a massa atômica, mas neste caso elas teriam que possuir uma carga muito maior que a carga elementar.
[3] Joseph John Thomson, físico inglês, 1856-1940.
Medida de e - Experimento de Millikan (1909)
Como discutido acima, para determinar separadamente a carga e a massa de uma partícula, é necessário utilizar outras forças, além da força eletromagnética. A força peso e as forças "macroscópicas", em especial a força de arraste no ar, são candidatas óbvias, mas torna-se então necessário estudar objetos bem maiores que as partículas dos raios catódicos. Nos seus clássicos experimentos, Millikan4 utilizou gotinhas de óleo e outros líquidos.
- O experimento procura determinar o valor da carga elementar e através do estudo do movimento de pequenas gotas carregadas sob a ação combinada da gravitação, do arraste do ar e de um campo elétrico vertical.
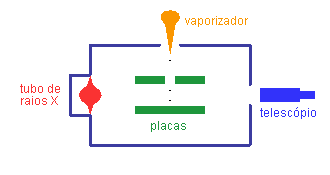
Esquema do experimento de Millikan
Veja o diagrama do experimento apresentado no artigo de Millikan.
- Sendo muito pequenas, as gotas possuam uma velocidade terminal muito pequena e a alcançam muito rapidamente. Nestas condições, a força de arraste pode ser considerada, em boa aproximação, como proporcional à velocidade:
onde o coefficiente b é proporcional à viscosidade h do ar e depende da geometria da gota. Para uma gota esférica de raio r, b é dado pela lei de Stokes:
(1-20) 
(1-21)
- Eliminando b entre (1-23) e (1-26), pode-se escrever
Observa-se a gota descendo uma distância L na ausência de campo elétrico e depois subindo a mesma distância L na presença do campo. Sendo Td e Ts respectivamente os tempos de descida e de subida, temos obviamente
(1-27)
e podemos re-escrever (1-27) na forma
(1-28) 
(1-29)
- No experimento de Millikan, a mesma gota era observada descendo e subindo várias vezes, sempre com o campo elétrico desligado nas descidas e ligado ao mesmo valor nas subidas. Entre subidas, a gota era irradiada por raios X, de maneira a modificar a sua carga elétrica. Se a carga muda do valor Q para o valor Q', a única quantidade que muda no lado direito da equação (1-29) é o tempo de subida e temos

(1-30)
- Se a carga for um múltiplo inteiro da carga elementar e,
a equação (1-29) poderá ser re-escrita na forma
(1-31)
Com a mesma hipótese, a mudança na carga entre subidas sucessivas será da forma
(1-32)
e a diferença entre as equações (1-30) e (1-29) tomará a forma
(1-33)
Comparando as equações (1-32) e (1-34), obtem-se a condição
(1-34)
Tendo medido Td, Ts e Ts', a tarefa é achar números inteiros n e Dn tais que esta igualdade seja satisfeita. Denotamos por C o valor comum dos dois lados da igualdade.
(1-35)
- Se conseguirmos determinar o valor da massa M da gota, poderemos finalmente determinar o valor da carga elementar através de
Sendo r a densidade do líquido utilizado, a massa de uma gota é dada em termos do seu raio por
(1-36)
Para determinar o raio, utilizamos a fórmula de Stokes. De (1-23), (1-37) e (1-21), obtemos
(1-37)
que permite calcular o raio da gota em termos de quantidades conhecidas ou medidas no experimento:
(1-38)
A massa da gota segue então da expressão (1-37).
(1-39)
- Veja um exemplo numérico.
Veja uma simulação do experimento de Millikan.
[4] Robert Andrews Millikan, físico americano, 1868-1953.






